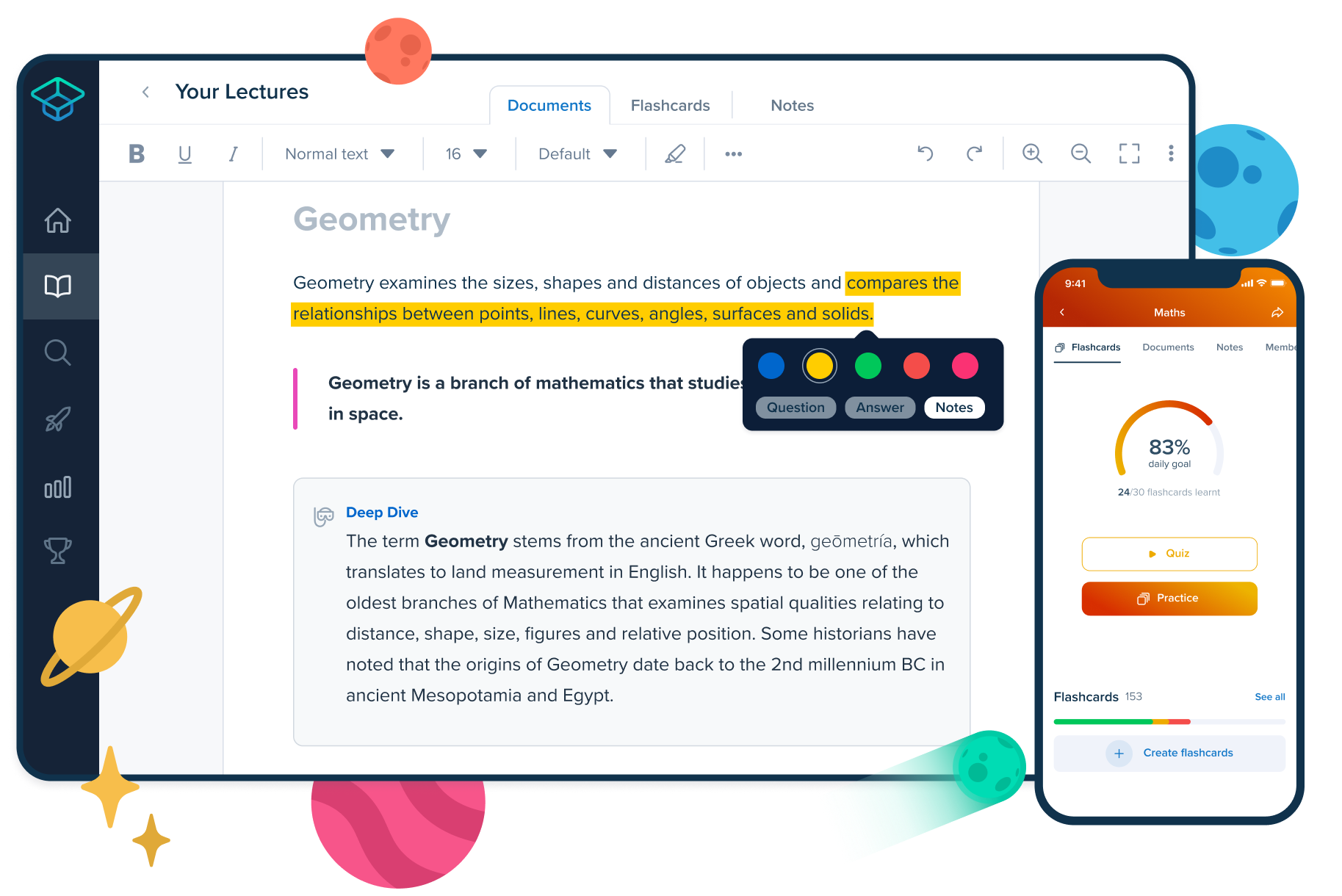
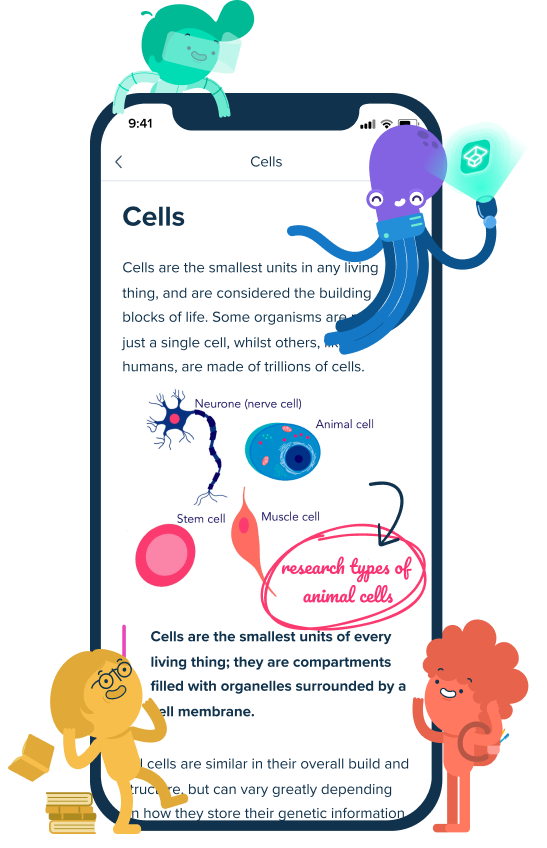
Feel at ease about exams with study sets verified by teachers
Our free StudySmarter Original study sets with explanations, FAQs, and flashcards are made for your courses and exams. Learning has never been easier with everything explained step by step by our subject-matter experts!
Get the app